“India beat Pakistan after ruthless Rohit Sharma sets insurmountable target at Cricket World Cup” — The Telegraph
“India vs Pakistan: Rohit Sharma’s 140 sets up victory for Virat Kohli’s side” — BBC Sport
”India vs Pak: Rohit Sharma smashes 140, his 2nd ton of World Cup 2019″— The Economic Times
I come into work, it’s Monday morning. Need coffee, head to the kitchen to make myself a cup.
Couple of my colleagues are already in, chatting around the water cooler.
As is norm in an Indian office, cricket is at the top of everyone’s minds. The conversation turns to the match. India versus Pakistan. Arch rivals. Borderline enemies, quite literally.
A data engineer at the cooler makes a joke about databases, partitions and Indo-Pak relations, let’s pretend to laugh. Okay, I lied. I made the joke.
Don’t judge. Nothing like dark humor to brighten a Monday morning.
One colleague says that the match was won by MSD. Sure, if you say so.
Second one chimes in saying Sharma was the x-factor.
The third one just wants some coffee, never mind.
Now that I have some coffee in me, I start paying attention to the conversation. This whole idea of whether the prodigal Sharma was just lucky or whether he had the required form to hit a 140 is an interesting concept. How would I figure this out? The analyst in me finally wakes up to the problem statement. Yesssss. Finally.
Drum roll please. Drums roll.
Enter the Bayesian hierarchical modeling technique.
What are the chances, Mr. Sharma?
Sport analytics literature says that the average runs in an innings in Cricket can be ideally modeled with a Negative-Binomial distribution. This is something they found out in like 1977 or something. Nerds, I tell you.
This is where it gets a little nerdy. A little why-are-you-making-me-do-so-much-math-y. A little ugh-y. I really need to stop trying to rhyme.
This distribution has a couple of interesting, intuitive properties. Imagine a Poisson distribution where the variance is not quite equal to the average runs. Makes sense for a set of cricket innings, no?
For all the non-math people (aka 98% of the world), essentially this means we are modeling for count data (i.e., runs) where the average number of runs might be more or less static but the amount of variance is highly volatile, and not quite the same across all games.
A negative binomial distribution has two parameters. One for the Poisson distribution, that models the average.
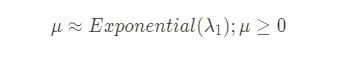
The second is for a gamma-distribution that models the variance.

The final model can be summarized as
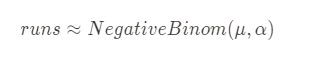
Note that we still haven’t taken into account the form and luck of the player.
I got all the batting scores Sharma had ever scored against Pakistan or had scored in 2019 (thanks, CricInfo, a couple of python scripts to pull the data from their databases did the job), and ran it through this very simple model over 10,000 simulations to get the posterior distribution.
Non-math definition: probable predictions with ranges.
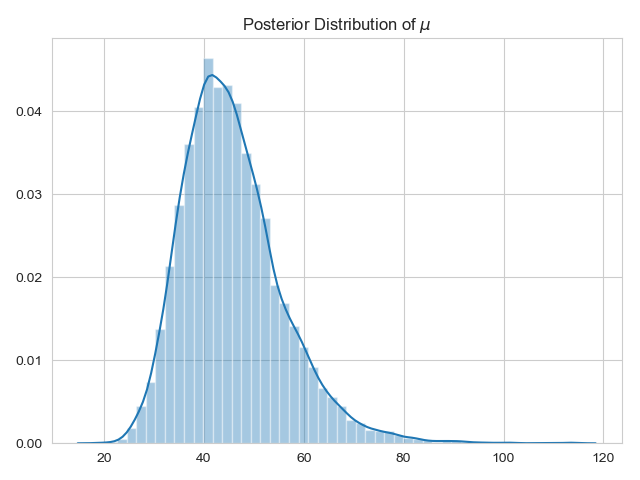
Posterior Distribution for the Average Runs/Innings
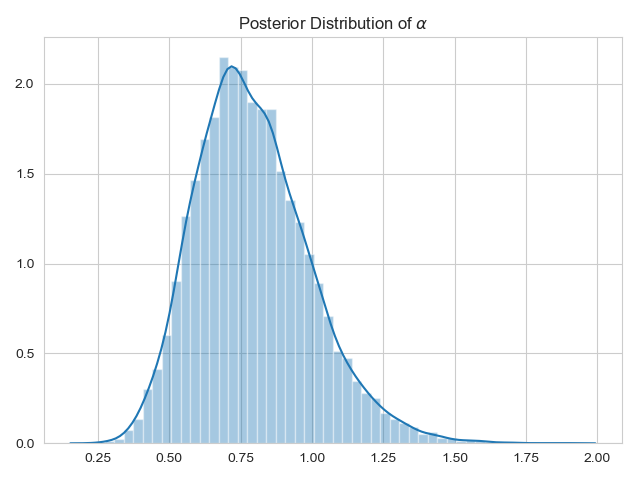
Posterior Distribution for the variance
Indeed, running a summary on the model shows that Rohit Sharma’s true average of runs in an innings is closer to 50, with an upper cap at 65–70. Having a wide-distribution for the alpha parameter would also indicate a high amount of uncertainty in the variance of runs, which could be a clue towards some of his runs being driven by luck.
We simulate Rohit Sharma’s batting 50,000 from the posterior distribution to try and evaluate the survival curve for Rohit Sharma.
(Non-math definition: What are the chances of the player being not out at greater than 10 runs, greater than 20 runs, greater than 100 runs, etc.)
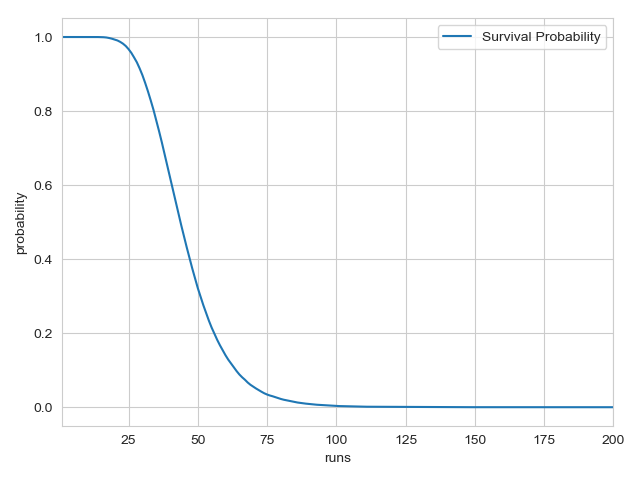
Here comes the clincher: the chance that Rohit Sharma could’ve scored 140 in this game is 0.00016.
One might debate/hate on the analysis with “Rohit Sharma’s form might have played a role in the 140 bro. Have you factored that in bro? How are you tackling that bro? You suck bro”
This is where Bayesian modeling gets interesting. Cue drum roll.
I should really hire a drummer-on-demand.
Is today your lucky day?
First off, no. If you’re this optimistic in life, you need help. A lot of it.
Secondly, and more to the point, how would we model luck and form? Intuitively, they are factors that affect the average of the player. In a multiplicative manner.
So, the average can essentially be modeled as
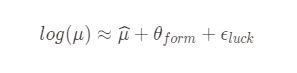
where the theta is the form and epsilon the luck component. The mu-with-a-cap term is the true average of the player.
We force a zero-sum constraint on the form and luck elements which means they are always in relation to the average form or luck across the matches, and hence more interpretative.
The thetas are drawn from standard normal distributions.
Having a log-linear model also allows the likelihood function to be better defined.
How does this model fit?
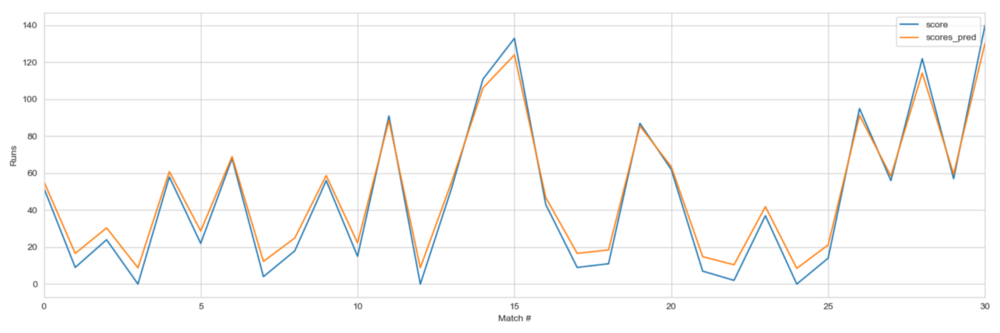
Not bad.
We model the scores in each of the innings against Pakistan and the predicted scores are pretty much in line with what actually happened.
Let’s decompose by form and luck and evaluate what happened in Match 30 (India vs. Pak, 2019)
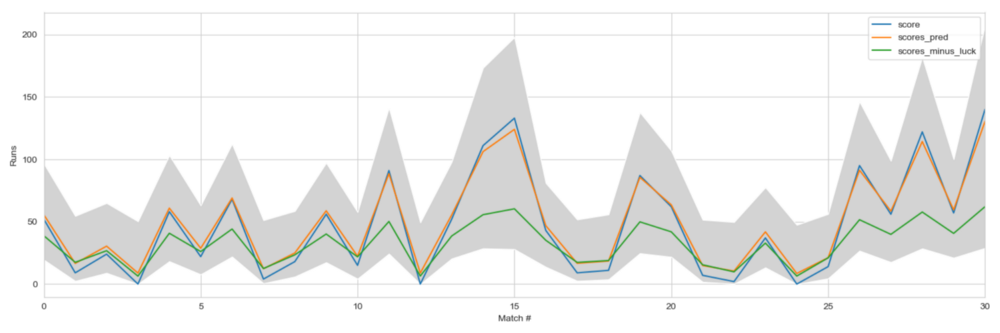
We see that Rohit Sharma would’ve probably scored around 62–65 had it not been for luck in the game. The green line effectively shows the form of the player for the given dataset.
Regardless of the implications of such an analysis, it sure will make the conversations around the water-cooler more interesting!
Drop a comment regarding questions, feedback, free cookies, anything.
This article was published with permission from the author. You can find the original article here.




