Imagine you have a magical coloring book, and you want to color each page using crayons. The first page has only a 2×2 grid of squares, so you easily color it with four different crayons.
As you keep turning pages, the grids get larger and larger, 3×3, 4×4, and 5×5 for respective pages. With each page, finding the right crayons becomes increasingly challenging and tedious.

Just like coloring larger grids becomes increasingly challenging, dealing with high-dimensional data becomes progressively more difficult for ML algorithms. As the number of dimensions in your data grows, the data becomes sparse, and the volume of the data space grows exponentially. With limited data points, it becomes harder for algorithms to capture the patterns, find relevant information, and make accurate predictions, just like it becomes tough to color larger grids with precision using only a few crayons. This issue of mining true information in a data set with multiple dimensions is the Curse of Dimensionality.
Explaining the curSe with a curVe
This sixth-grade experiment to measure the length of a curved line hits the nail on the head.

Common sense dictates that measuring the distance between A and B using the scale does not give the actual length. Instead, we place a thread on the line, and bend the thread to the shape of the line, and then mark points A and B. This thread is then laid out straight and the distance between the two points is measured using a ruler.
How does this relate to the AI field? It messes up an AI’s capability to judge the data sets. It leads to increased computational complexity and overfitting. Here’s an illustration to show how the interpretations may vary as more dimensions get added
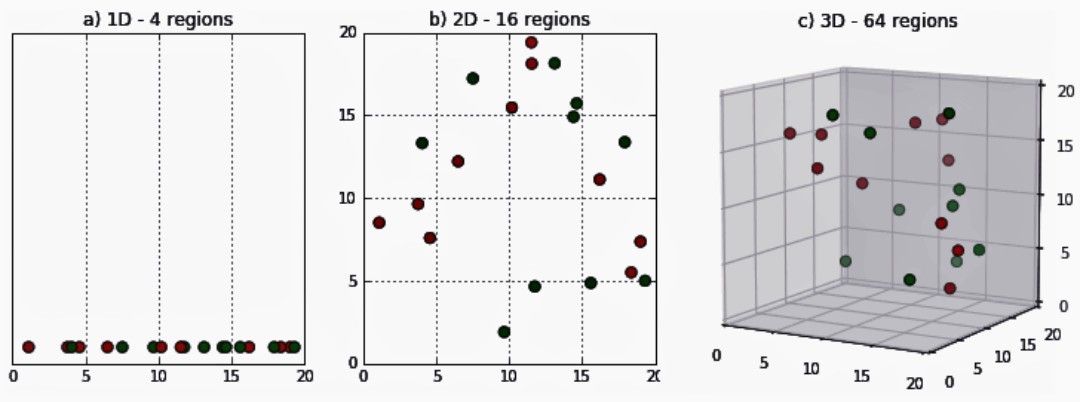
Source: DeepAI.org
How to deal with it?
A combination of these methods may be required to effectively dispel the Curse of Dimensionality:
1. Dimensionality Reduction: Techniques like Principal Component Analysis (PCA) help compress the data while retaining most of the important information.
2. Manifold Learning: Such algorithms can identify the intrinsic lower-dimensional structure of the data, thus allowing a reduced and more informative subspace.
3. Binning or Discretization: Grouping continuous values into bins can aid easier analysis.
4. Regularization: In machine learning models, using L1 or L2 regularization techniques can reduce the impact of irrelevant features and bring down the dimensionality.
5. Curse-Aware Algorithm Design: Develop algorithms that are specifically designed to handle high-dimensional data efficiently and gracefully.
6. Generative Models: Use generative models like Variational Autoencoders (VAEs) or Generative Adversarial Networks (GANs) to learn a compressed and meaningful representation of the data.
























